A Proposal for the Intercomparison of GCM Dynamical Cores with Stochastic Perturbations
with Stephan Juricke, Peter Düben, Tim Palmer
Motivation
- Large-scale numerical models use an approximation: Deterministic primitive equations are discretized and solved on grids.
- We don’t often account for this uncertainty in our models.
- Represent the inherent uncertainty in our solutions as stochastic terms.
- Stochastic terms also represent physics (e.g. Brownian motion)
Exact equations for a GCM
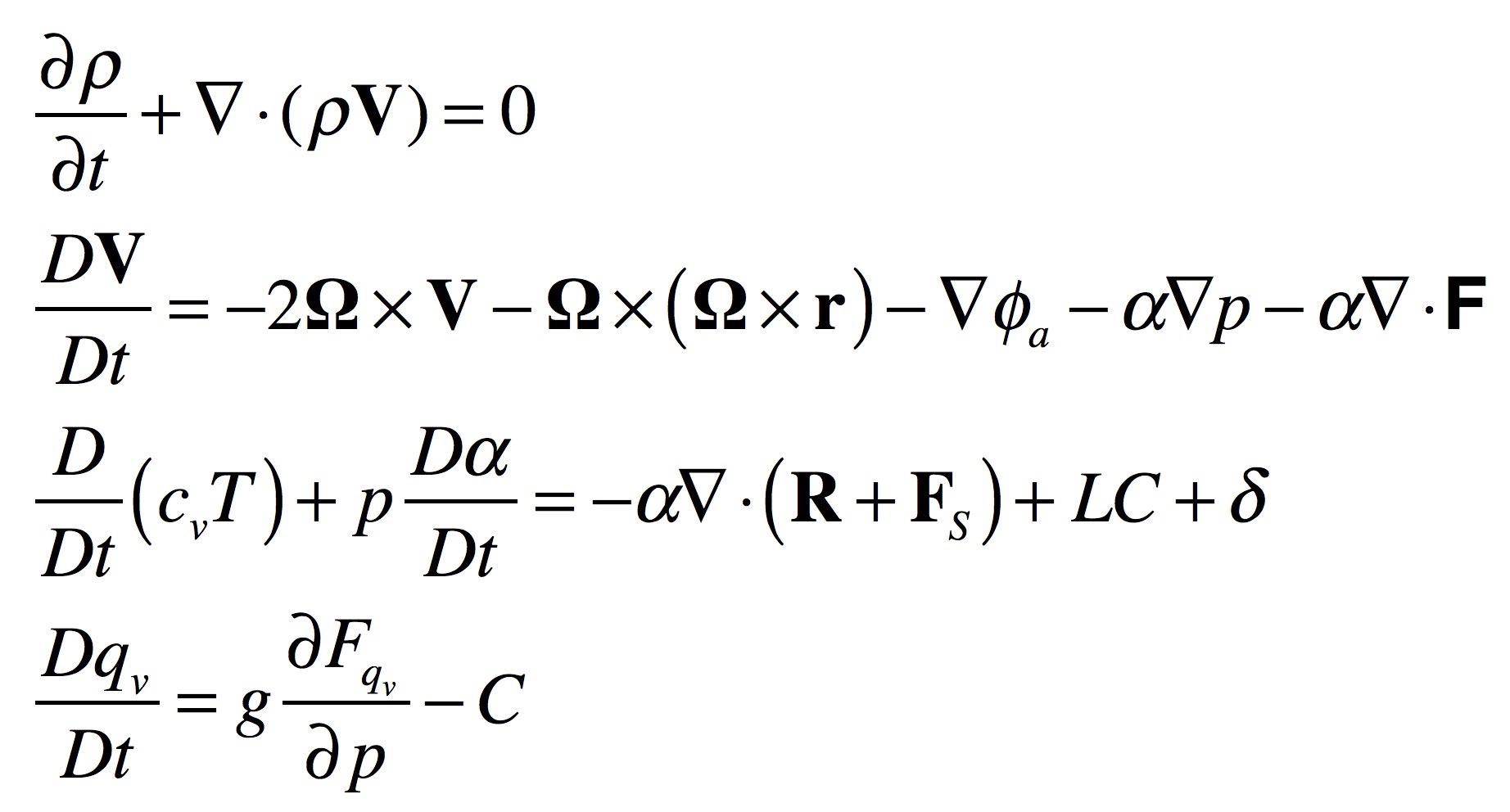
The exact equations are known except for some caveats.
Approximations
|
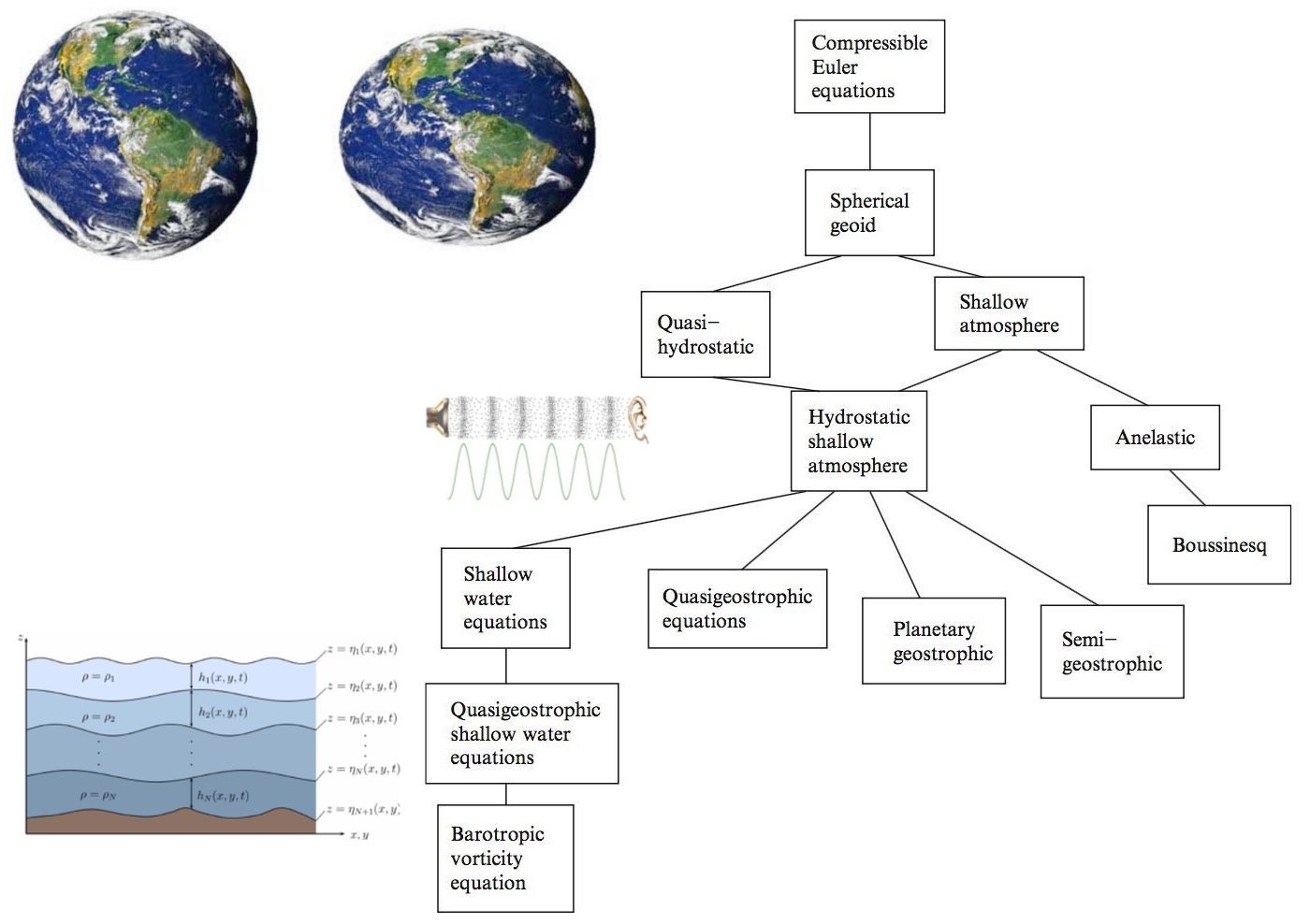
|
Physics-dynamics coupling
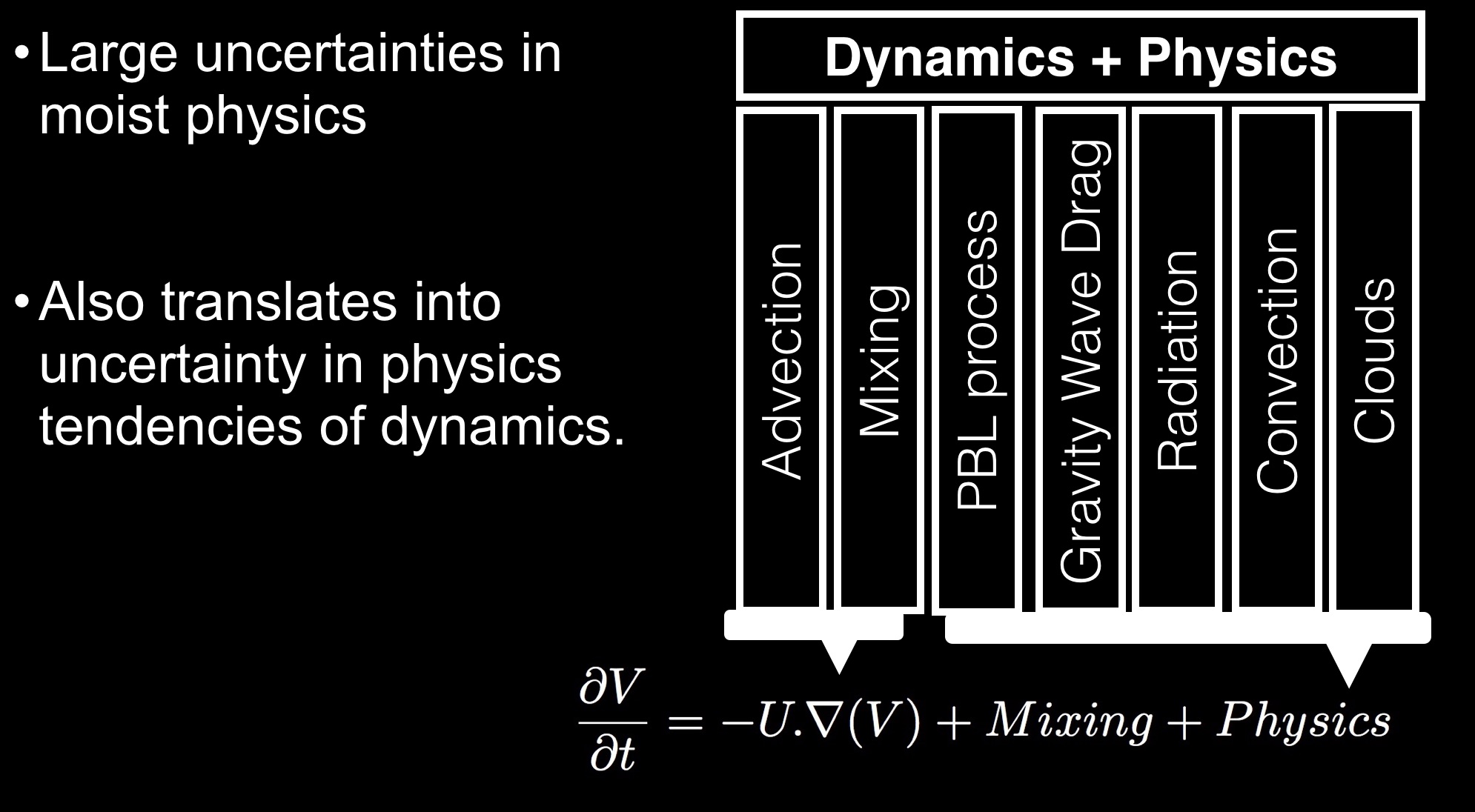
Dynamical Cores
Dynamical Cores

Dynamical core intercomparison to evaluate their performance should also consider their inherent uncertainty.
Sources of uncertainty
- Parameterized diffusion
- Numerical discretization
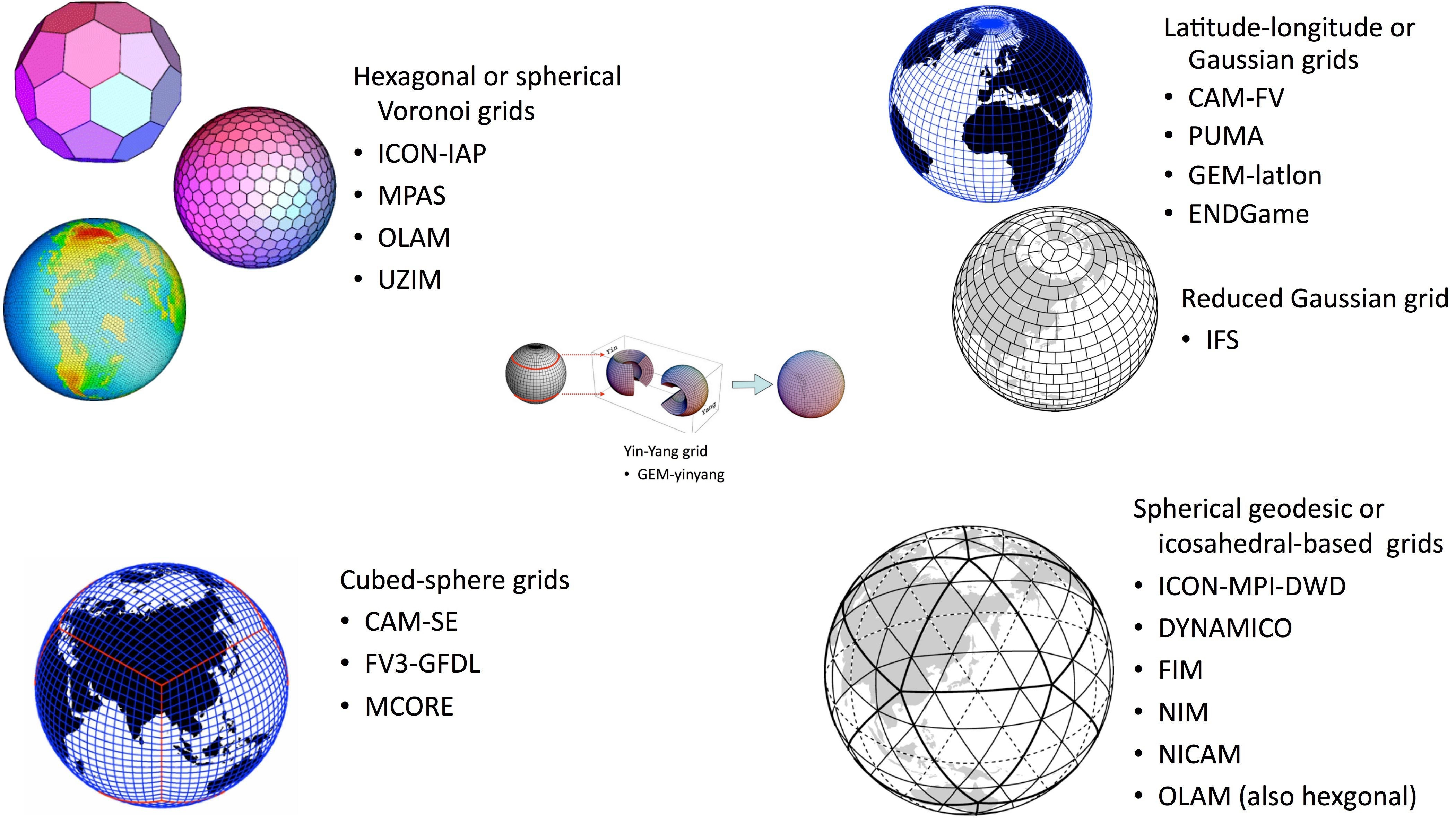
- Choice of grids
- Physics tendencies of dynamics, orography, sub-grid processes.
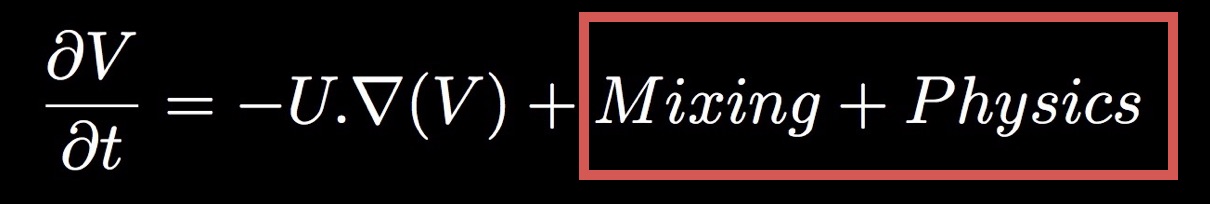
$$\frac{\partial u_j}{\partial t} + \frac{\phi_{j+1} - \phi_{j-1}}{2\Delta x} = 0$$
Our proposal
- In our inter-comparison test cases, include uncertainty representation in the dynamic tendencies.
- This uncertainty can be represented as an additive stochastic term in the equations
- Dynamical cores which differ in performance despite this representation of uncertainty can be evaluated to perform differently.
The "fruit fly" of climate models
Held-Suarez Testcase
- 1500-day integrations : assessment of climate statistics
- Simplified physics - temperature relaxation function and Rayleigh friction for the wind in lower levels.

Simplified physics
Radiation and convection parameterized as
$$Q = -\kappa(T-T_{eq})$$
- Warmer than Teq => cooling
- Cooler than Teq => warming
Model initialised at T = 255 K uniformly everywhere.
U, V = 0 everywhere. Resolution: T159.
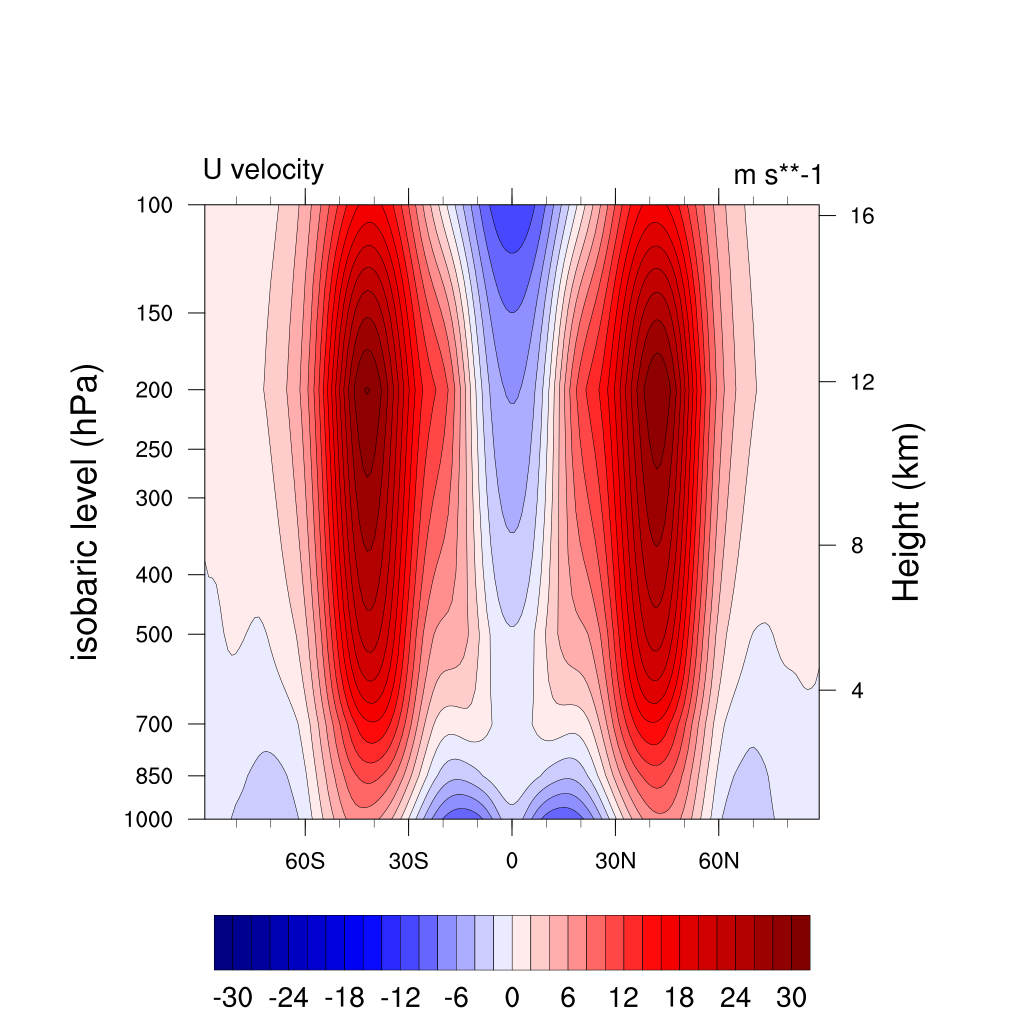
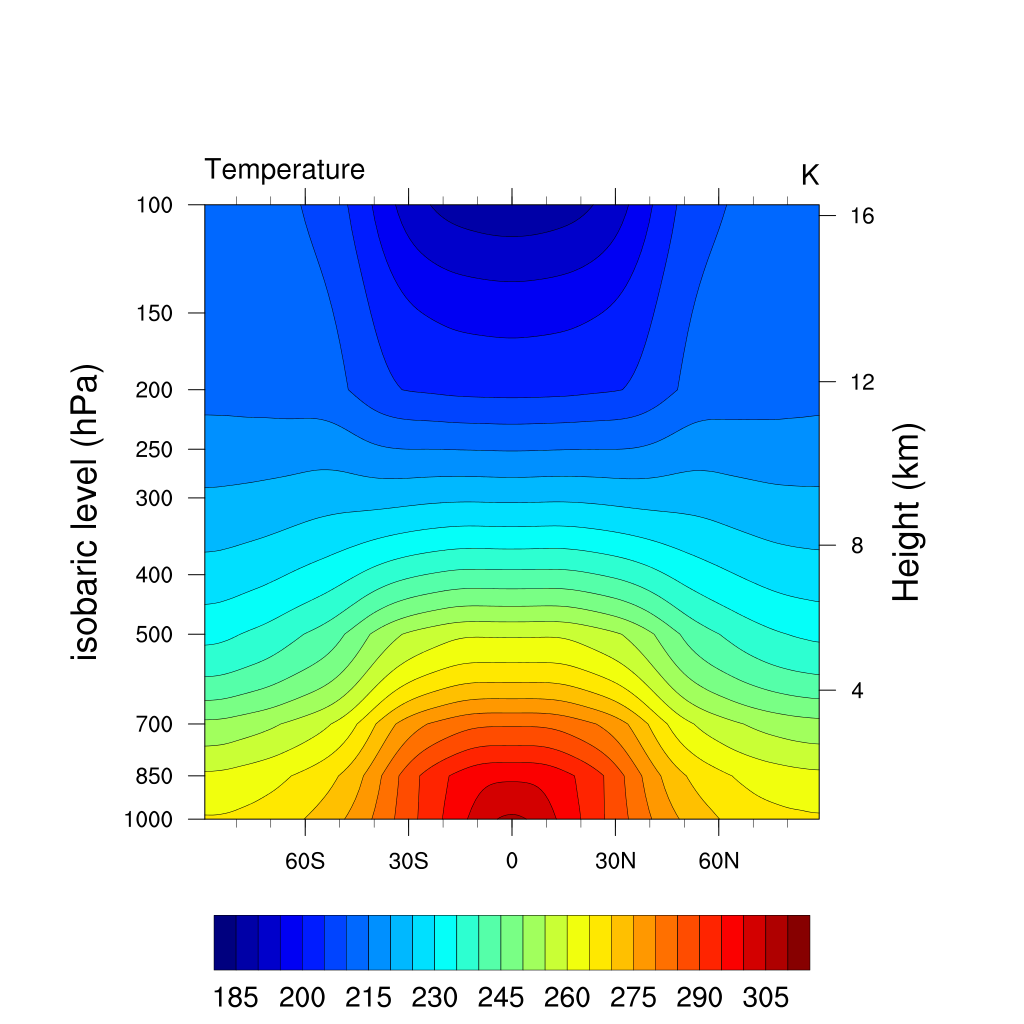
Zonal winds and temperature
Mean winds and temperature over last 1000 days of 1500 days simulation
Generic form of Explicit Diffusion Mechanism
$$ F_\psi = (-1)^{q+1} K_{2q}\nabla^{2q}\psi $$
where $q>1$ is a positive integer, 2q - the order of the diffusion, $K_{2q}$ - diffusion coefficient and $\nabla$ is the gradient operator.
We now compare the use of biharmonic (q=2) and hyper (q=4) diffusion in a Held-Suarez testcase.
Zonal wind comparison
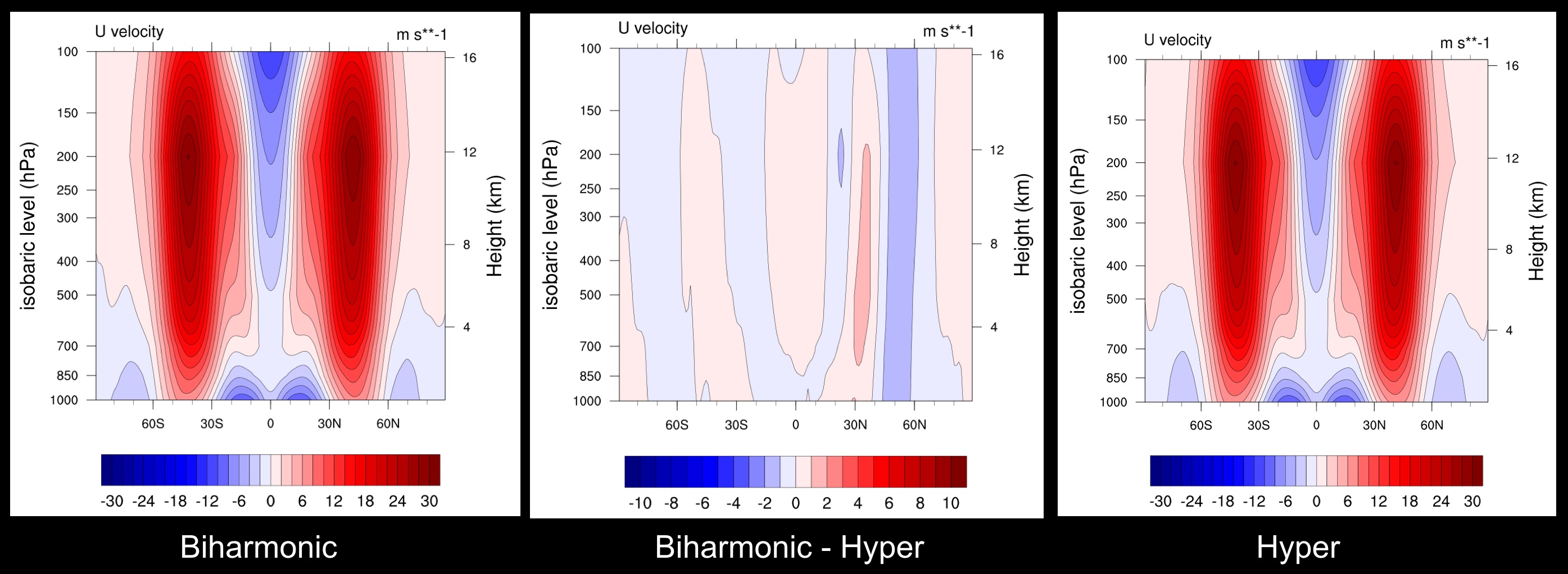
Uncertainty in the diffusion operator translates into uncertainty in model solution
Meridional Eddy Heat Transport: $ \overline{V'T'}$
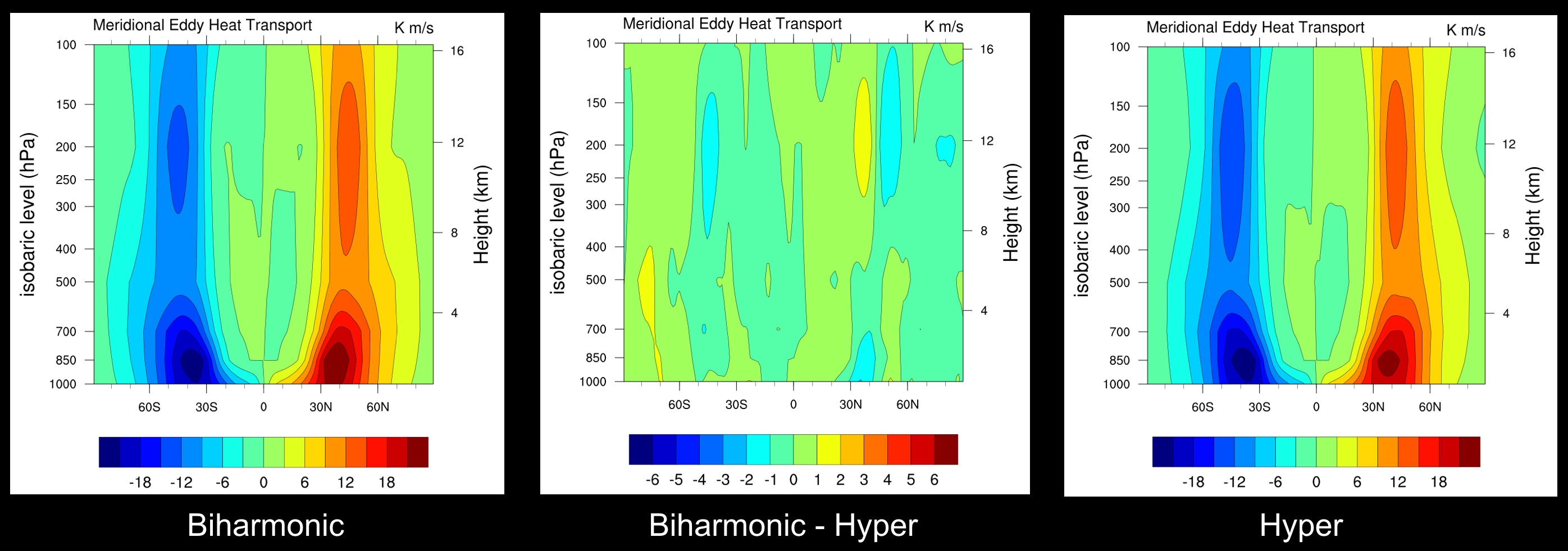
Uncertainty in the diffusion operator translates into uncertainty in model solution.
Kinetic Energy Spectra
700 hPa Kinetic energy spectra (bi-harmonic vs hyper diffusion)
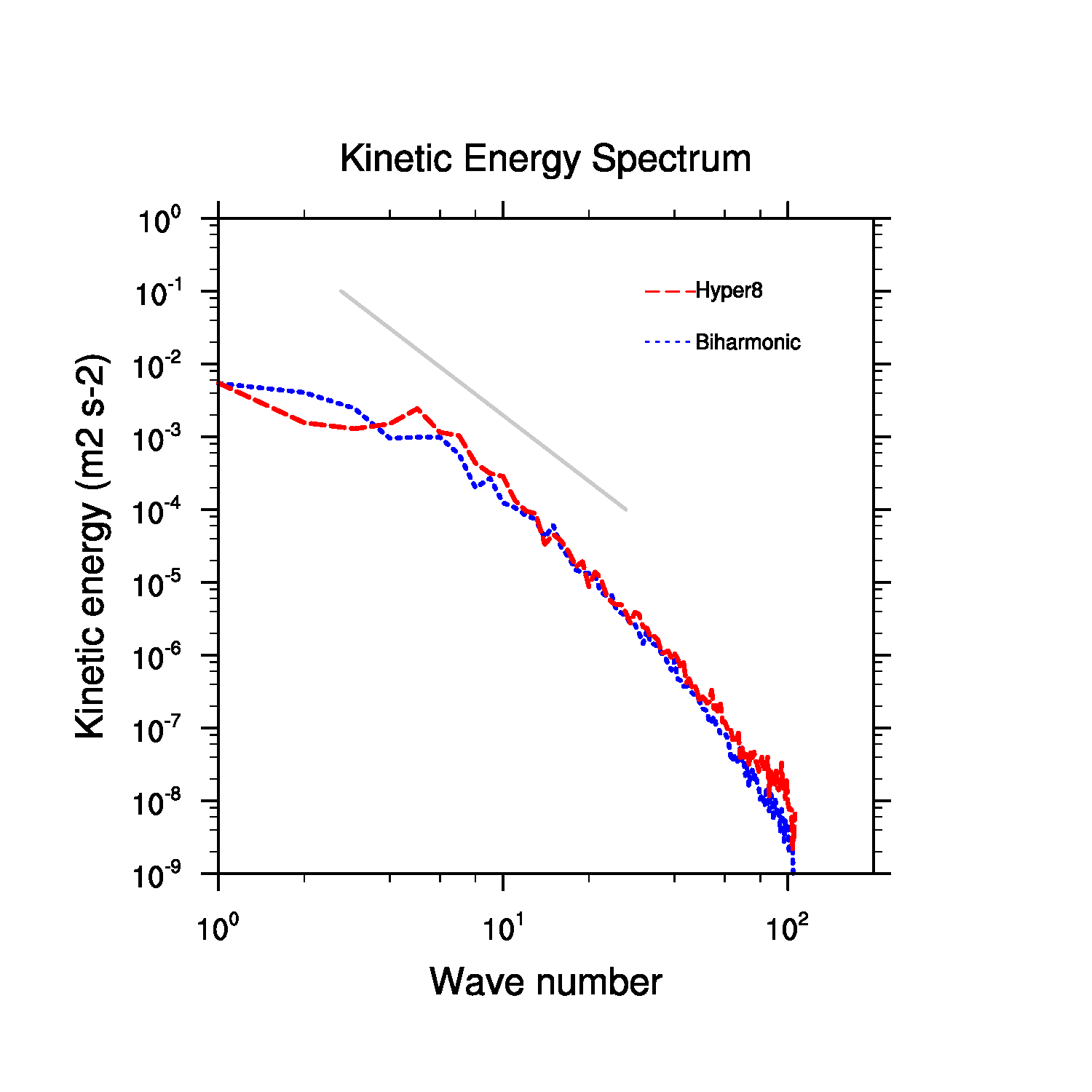
The kinetic energy spectra are comparable except at large wavenumbers, the hyper diffusion has lesser energy.
Stochastic Perturbations to Dynamical Core
Stochastic parameterization to represent model error
The net parameterized physics tendency: $$𝑿= 𝑋_U, 𝑋_𝑉, 𝑋_𝑇, 𝑋_𝑄$$ are perturbed with multiplicative noise $$𝑿′ = (1 + \mu 𝑟)𝑿$$
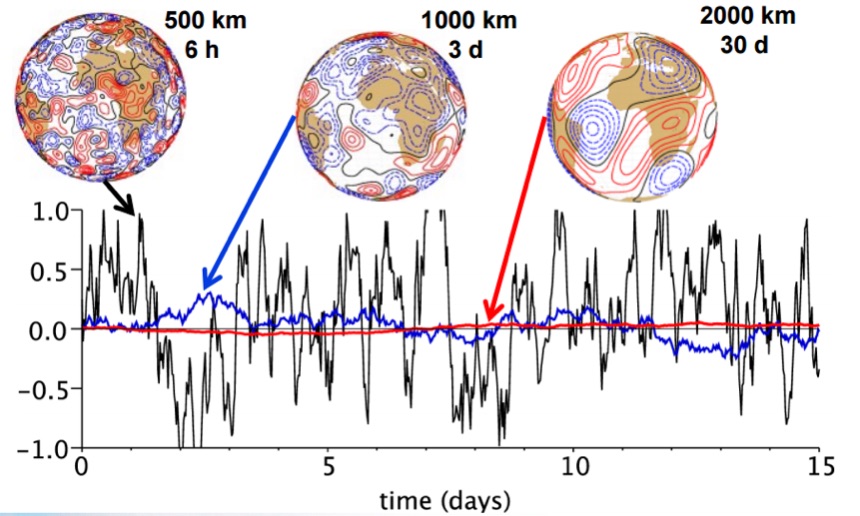
SPPT is currently implemented at ECMWF, NCEP, NCAR, UKMO, JMA and others.
SPPT Zonal Wind Tendencies
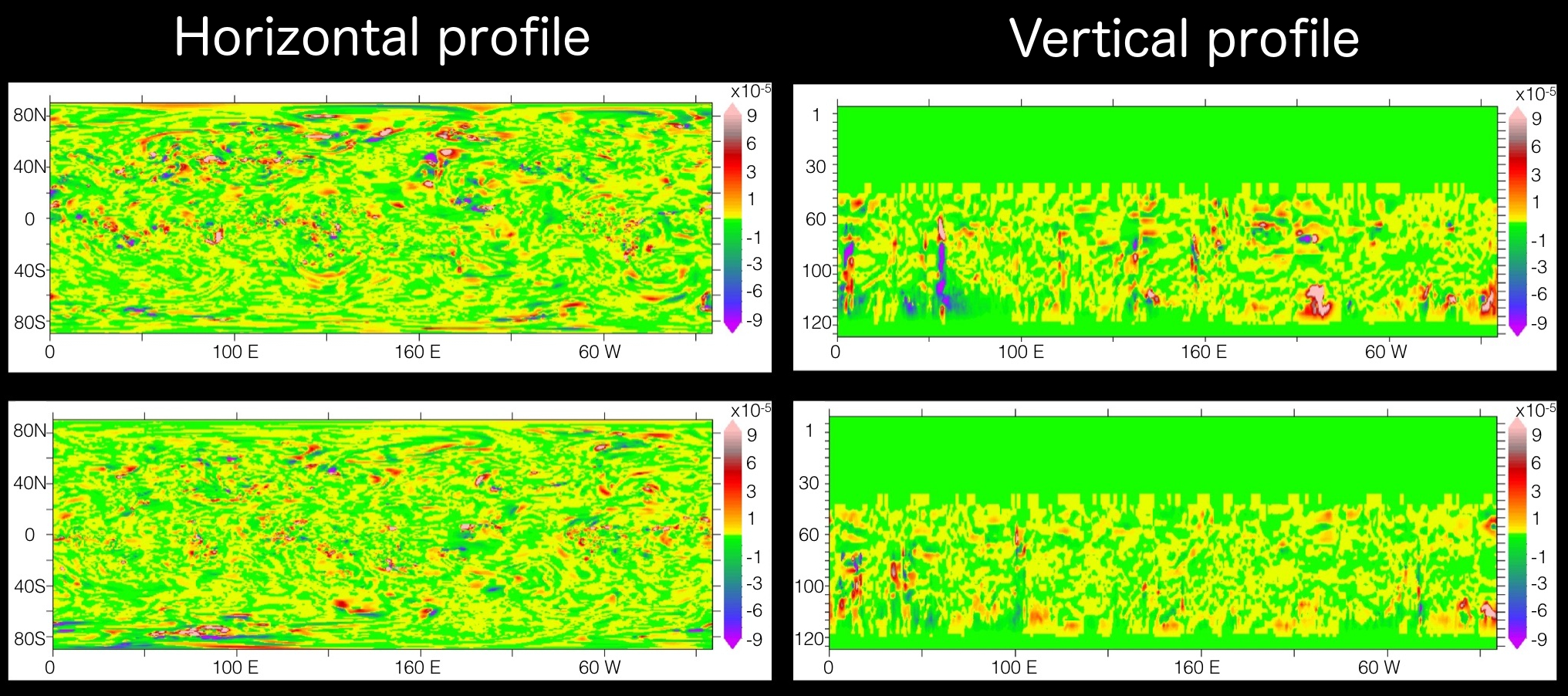
Stochastic tendencies of zonal and meridional wind saved from an aquaplanet simulation of ECMWF IFS
Additive stochastic forcing for dynamical core
$$\frac{\partial V}{\partial t} = - U . \nabla(V) + Mixing + \sigma \mathcal{N}(0,1)$$
!===================================================================================
! Stochastic Perturbations to U, V
!===================================================================================
IF (LHELDSUAREZ_STOCH) THEN
! WRITE(NULOUT,*) 'Starting Loop for stochastic forcing IBL:',IBL
! CALL FLUSH(NULOUT)
DO JK=1,KLEV
DO JL=KIDIA,KFDIA
PTENU(JL,JK) = PTENU(JL,JK) + TRLXQ(JL,JK,1,IBL)
PTENV(JL,JK) = PTENV(JL,JK) + TRLXQL(JL,JK,1,IBL)
ENDDO
ENDDO
! WRITE(NULOUT,*) 'Stoch update sucessfully finished'
! CALL FLUSH(NULOUT)
ENDIF
Zonal wind comparison
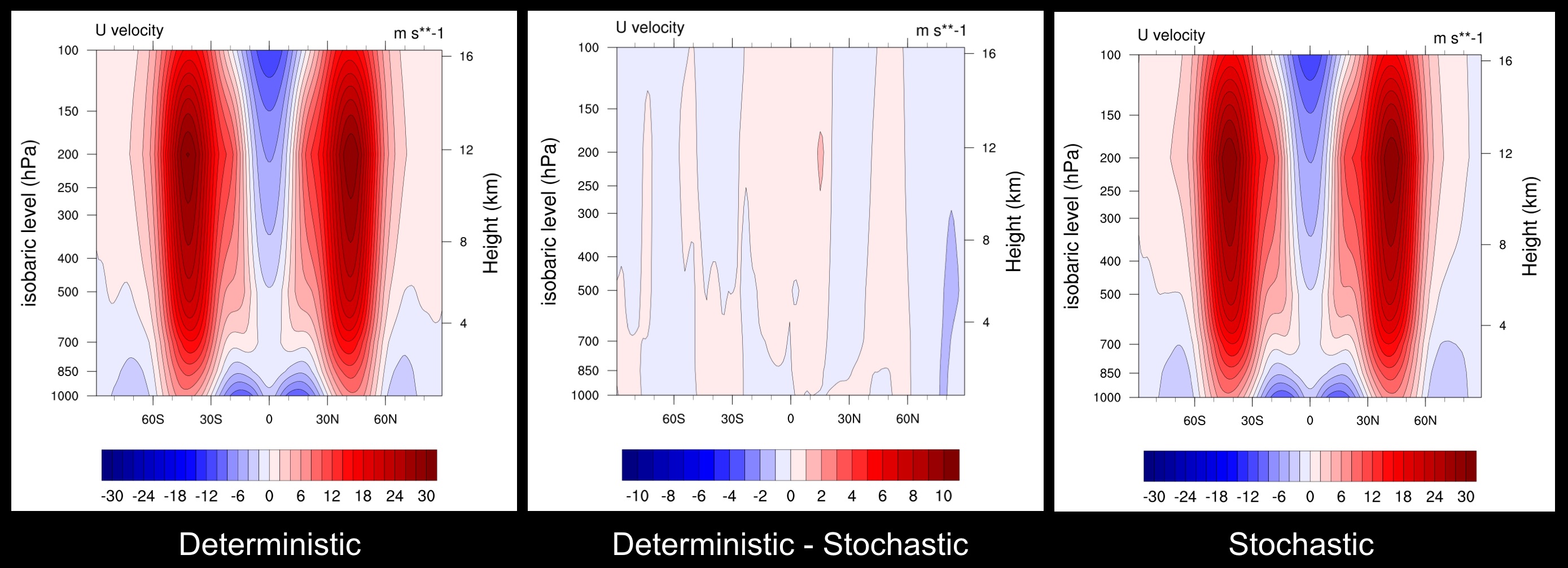
Stochastic (SPPT) perturbations to dynamical tendencies do not change the mean climate significantly.
Eddy Heat Transport: $ \overline{V'T'}$
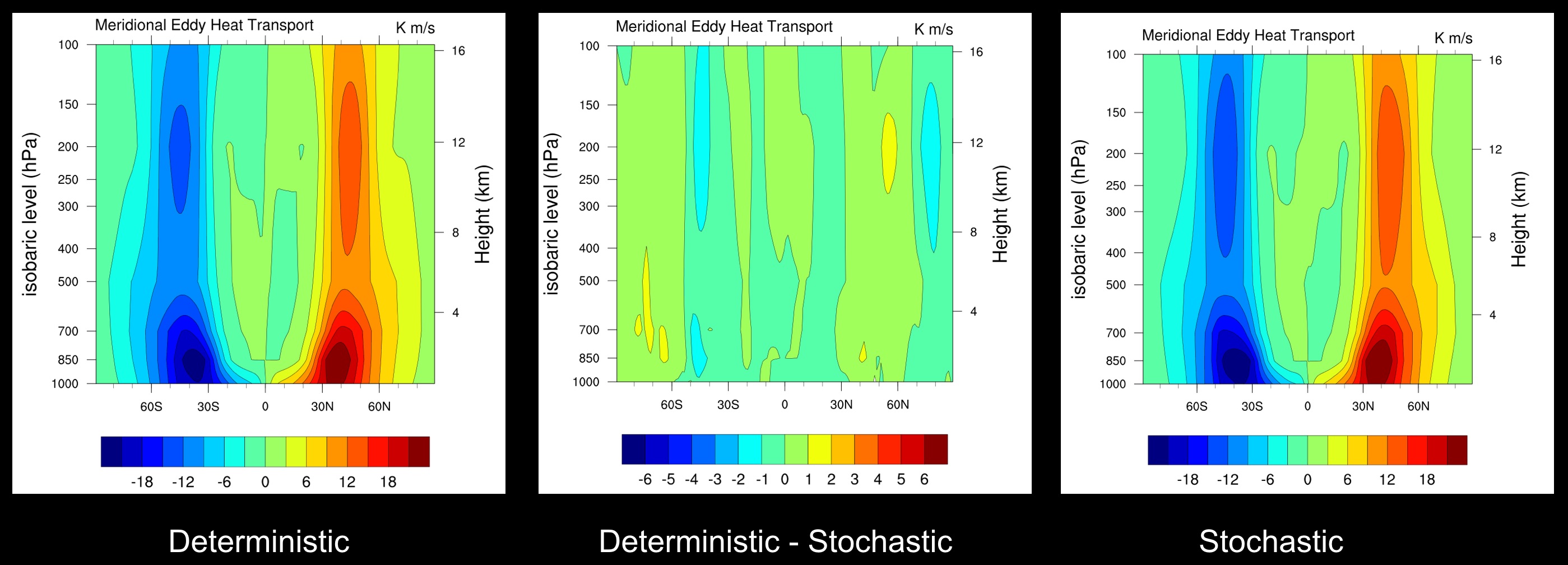
Stochastic (SPPT) perturbations to dynamical tendencies do not change the eddy variability significantly either.
Kinetic Energy Spectra
Kinetic energy spectra (700 hPa)
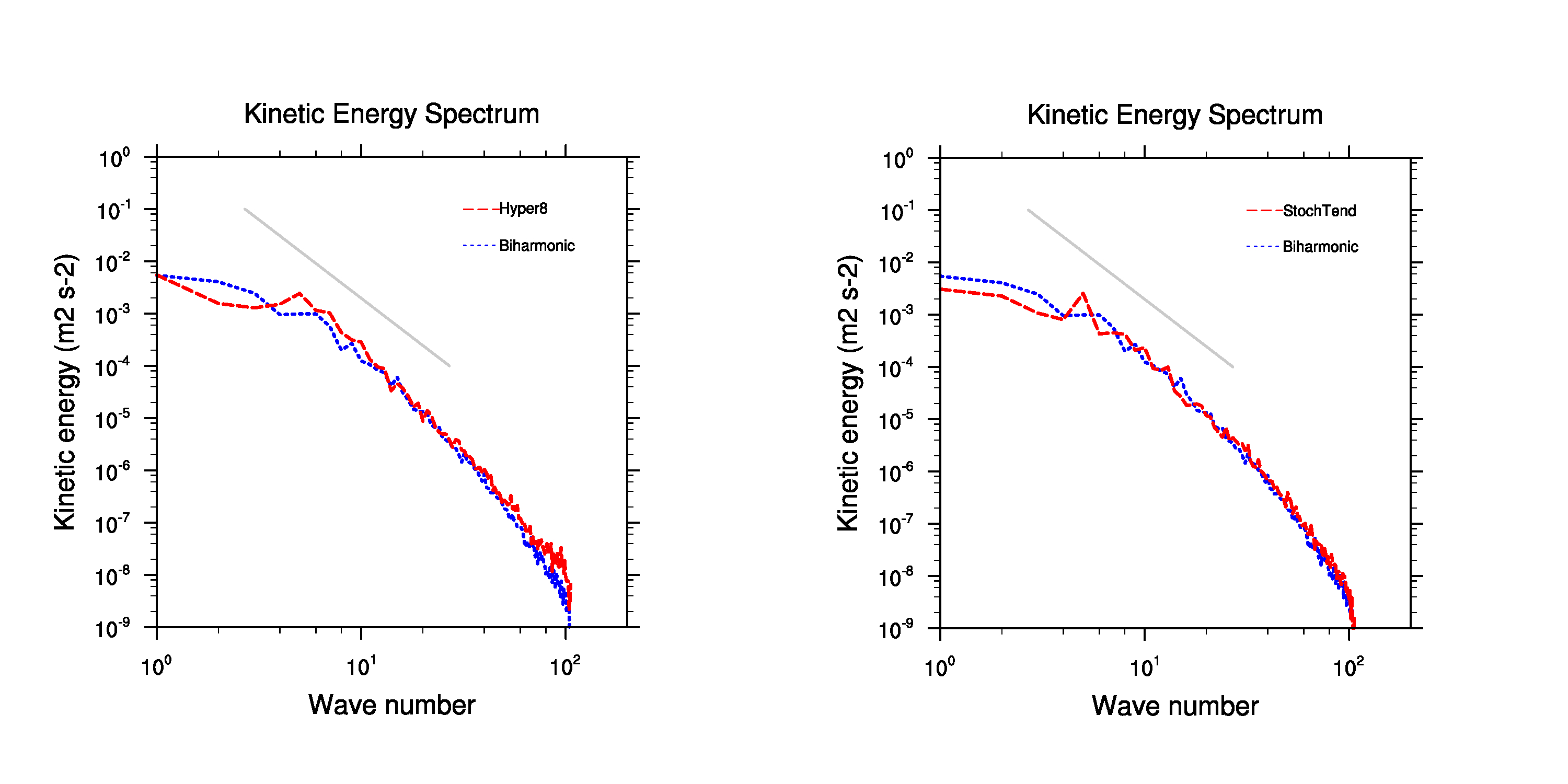
Stochastic perturbation run (right) comparable to the deterministic run (left)
Stochastic perturbations to diffusion coefficient
$$ F_\psi = (-1)^{q+1} K_{2q}\nabla^{2q}\psi $$
where $q>1$ is a positive integer, 2q denotes the order of the diffusion, $K_{2q}$ stands for the diffusion coefficient and $\nabla$ is the gradient operator.
Stochastic diffusion coefficient is given by
$$ F'_\psi = (1 + r \mu) F'_\psi $$ where r and $\mu$ are the random perturbations and standard deviation terms.
Zonal wind comparison
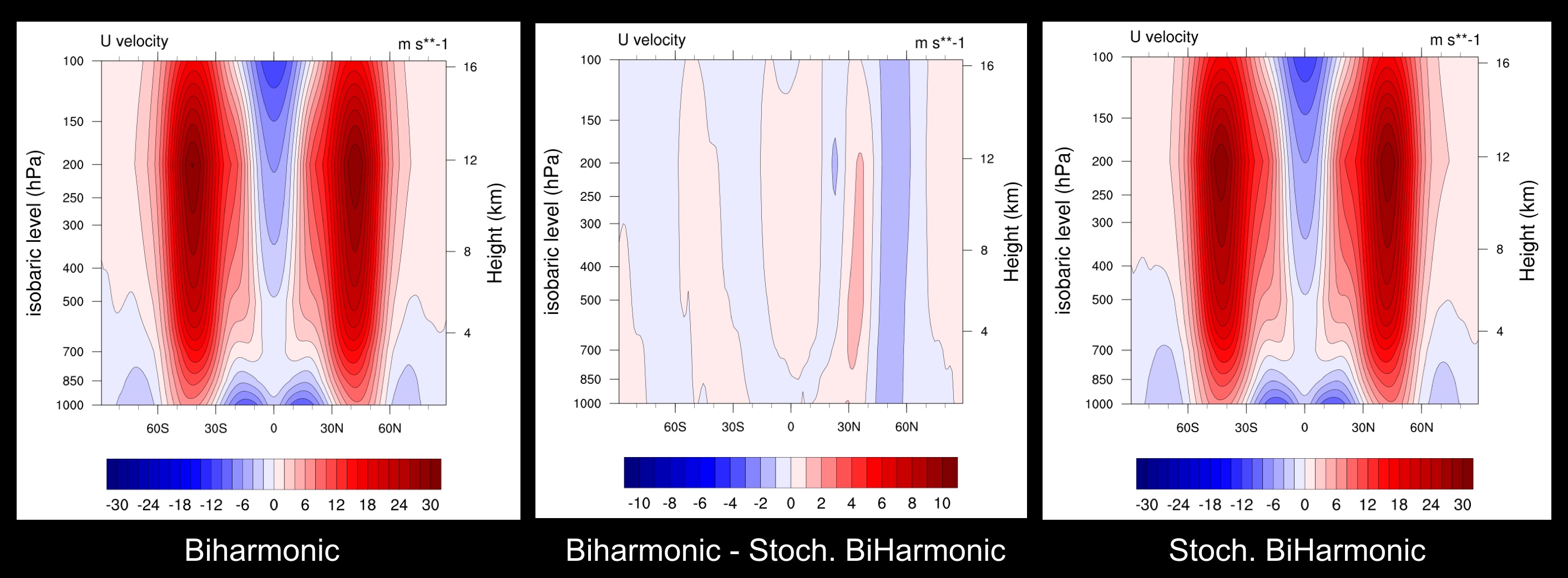
Stochastic perturbations to diffusion coefficient do not change the mean climate significantly either. Same order of magnitude as using a higher order diffusion
Eddy Heat Transport: $ \overline{V'T'}$
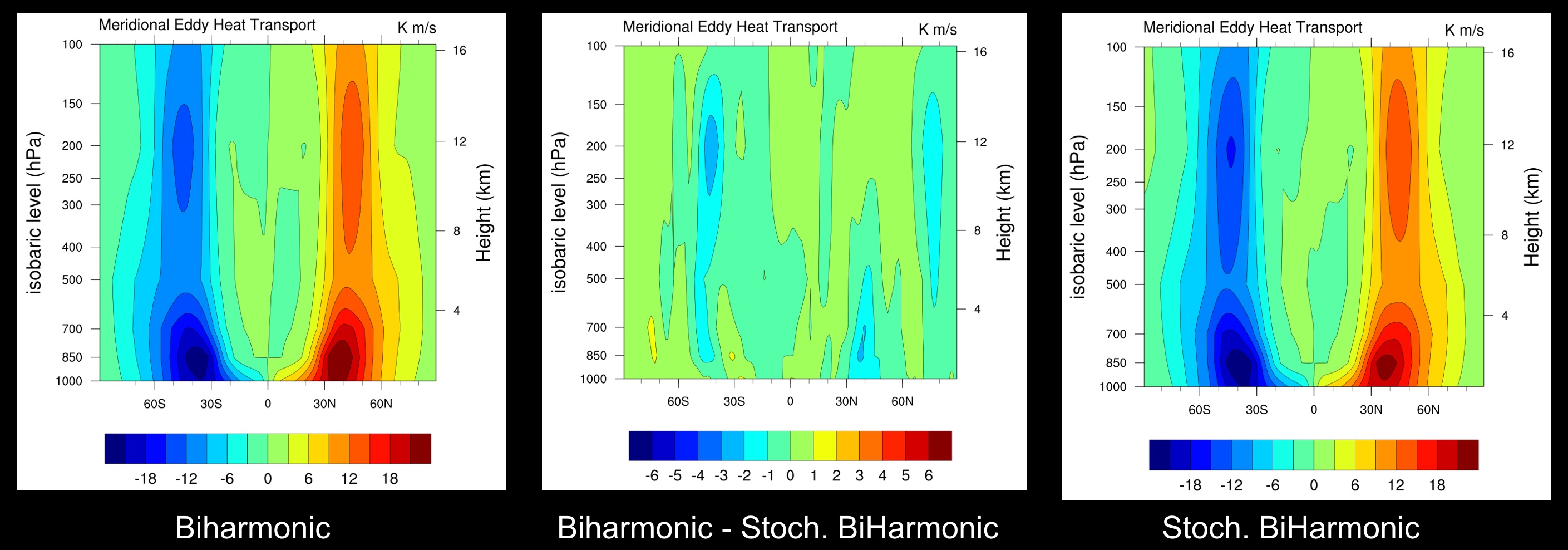
Stochastic perturbations to diffusion coefficient do not change the eddy variability significantly either. Same order of magnitude as using a higher order diffusion
Kinetic Energy Spectra
Kinetic energy spectra (700 hPa)
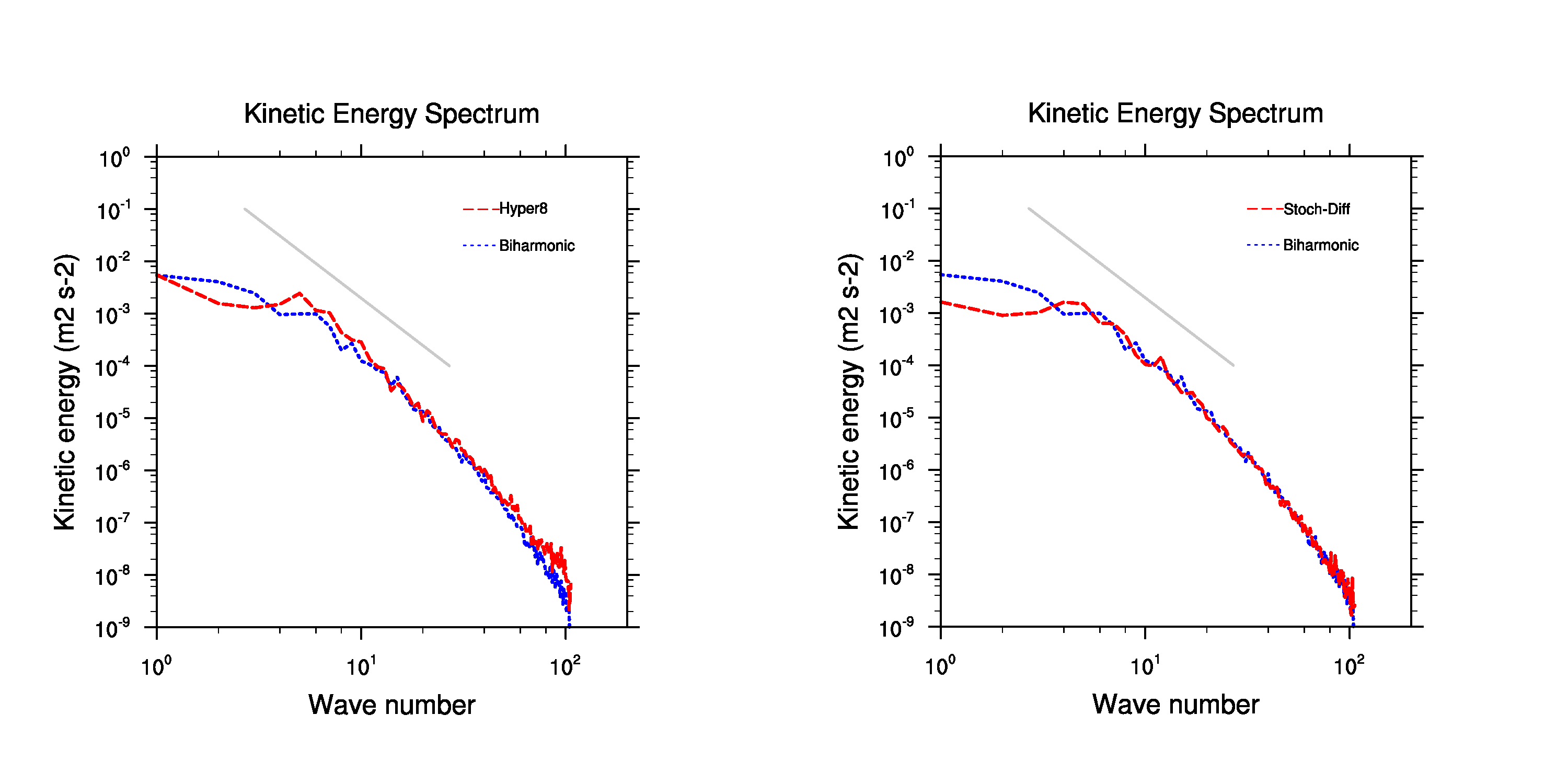
Stochastic perturbations to $F_\psi$ (right) is comparable to the deterministic run (left)
Summary
- Stochastic representation of uncertainty in dynamical tendencies from an operational weather forecasting model was used in an idealized test case.
- Changes in model mean and eddy variability due to stochastic forcing is of similar magnitude as using a different diffusion scheme
- We propose that uncertainty in dynamical tendencies be represented as "an additive stochastic term" in all dynamical cores in an inter-comparison study
- This will help evaluate the performance of dynamical cores in these tests in the presence of inherent uncertainty in the system
- Dynamical cores which differ in evaluation metrics despite this representation of uncertainty can be identified as performing differently

More accurate weather prediction with less precision
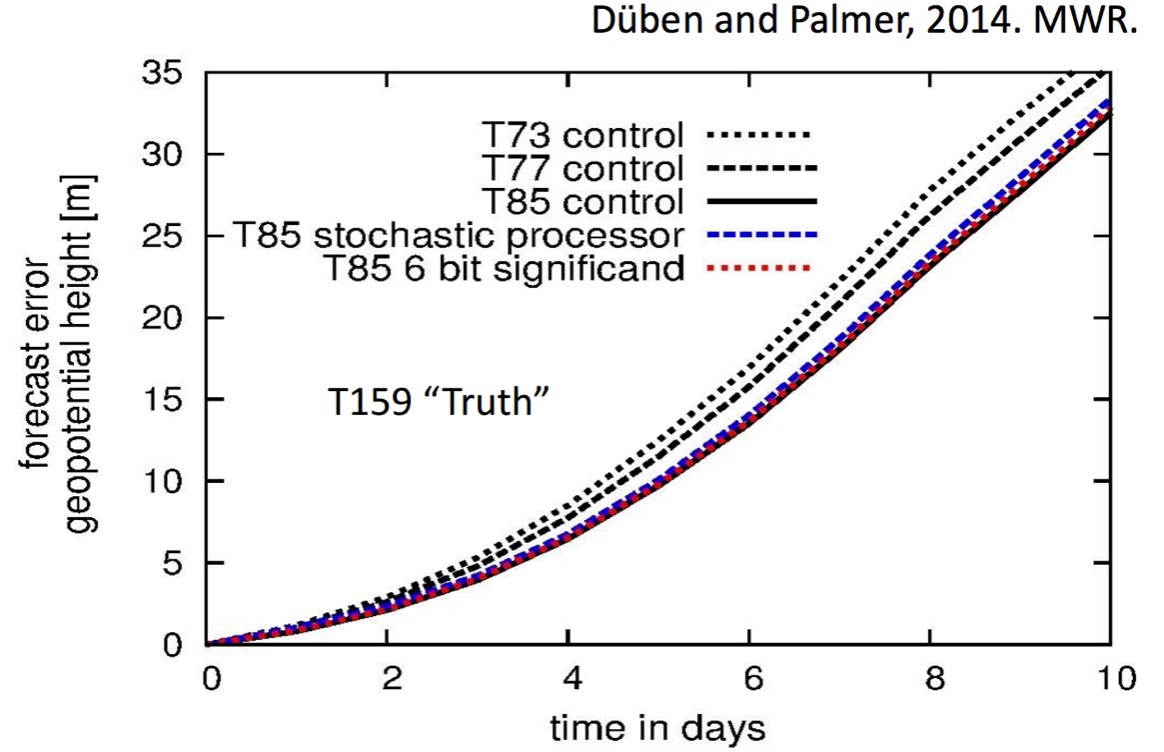
- The stochastic chip / reduced precision emulator is used on 50% of numerical workload: All floating point operations in grid point space.
- All floating point operations in the Legendre transforms between wavenumbers 31 and 85
- Imprecise T85 cost approx that of T73
Many thanks to: Sylvie Malardel, Filip Vana, Linus Magnusson (ECMWF)
Dynamical Core of IFS
- Hydrostatic primitive equations
- Reduced Gaussian grid (Horizontal) & Hybrid in vertical
- Spectral with a semi-Lagrangian, semi-implicit time discretisation
- Uniform spherical geometry and finite-element vertical discretization
- Horizontal Diffusion : dampen energy and enstrophy accumulation, absorb vertical waves at top of model, subgrid-scale mixing
Spherical coordinates: IFS